A deep dive into Scala's type system : Variance (part II) : Covariance

In the first part of the series, I started by examining the concept of variance and introduced invariance. A thorough reading of the first part is recommended for getting familiar with the terminology and the basic concepts.

This article describes another form of variance, namely, covariance.

Example

Nothing serves the presentation of new concepts better than examples, therefore I will continue with a concrete scenario.

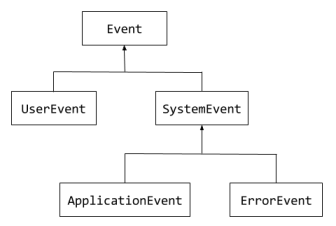
Imagine an event-driven software system. Such a system is based on broad categories of events, like events related to the functioning of the system (system events), events generated by user actions (user events) and so on.

An approach to model these events:

And a skeletal implementation in scala:

trait Event

trait UserEvent extends Event

trait SystemEvent extends Event

trait ApplicationEvent extends SystemEvent

trait ErrorEvent extends ApplicationEvent

As stated earlier, traits in Scala are a way to define types.

Since there can be many categories of events it would make sense to create separate event sources for each type. An event source will inherit from a generic trait, Source, that is parameterized. Also, the programmers have decided to make the type parameter covariant. A covariant type parameter is created by marking the parametrized type with +.

trait Source[+Out] {
  def get(): Out
}

Some concrete event sources :

trait UserEventSource extends Source[UserEvent]

val ues = new UserEventSource {
  override def get(): UserEvent = ???
}

trait SystemEventSource extends Source[SystemEvent]

val syes = new SystemEventSource {
  override def get(): SystemEvent = ???
}

In reality there should be more event sources in the system. In this fictional example, an UserEventSource and a SystemEventSource are all that is needed. Note also that the actual implementations are omitted (by using the ??? symbol).

At some point, our requirements dictate that we need to intercept and forward events to another parts of our system, which are interested in those events (in order to log them, or use them for other purposes).

So a method is written to handle this scenario.

def forwardEventsComingFrom(source: Source[Event]): Unit = {
  // imagine events are continuously intercepted as they arrive
  source.get()
  // and then forwarded
}

This method is declared to accept a source of Events as a parameter. The designer of this method has taken advantage of the fact that Source is declared to be covariant, therefore the following calls are legal :

forwardEventsComingFrom(ues)

forwardEventsComingFrom(syes)

Covariance explained

Note that both UserEventSource and SystemEventSource can be passed as parameters to the method.

How is this possible?

Covariance refers to the possibility to substitute a type parameter with its subtype.

Even more, the covariance annotation makes it possible to create a type hierarchy between parameterized types that is parallel to the type hierarchy of the types used as parameters.

By relaxing the invariance constraint, both Source[UserEvent] (UserEventSource) and Source[SystemEvent] (SystemEventSource) become subtypes of Source[Event] and thus are accepted by the compiler. Therefore, covariance can also be thought of as a ‘narrowing’ relationship, since types are ‘narrowed’ from more generic to more specific.

In the current situation, the direction of inheritance between parameterized types like, Source[UserEvent] and Source[Event] is the same as the direction of inheritance between UserEvent and Event, as depicted in the following diagram.

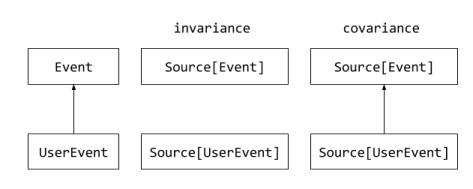
Hence the name, covariance.

Formally, if a type is covariant, then, assuming existing types T, A, B, if T[B] conforms to (is assignable to) T[A] then A must be the super type of B.

Conformance follows the direction of inheritance, therefore, the following statement would compile: val v: Source[Event] = ues

In case of inheritance, covariance allows subclasses to override and use narrower (or more specific) types than their superclass in covariant positions as the return value.

Closing remarks

This article explained and demonstrated covariance via a practical example. The next part will discuss discuss another incarnation of variance, namely, contravariance.